Книга: Ферма П. «Исследования по теории чисел и диофантову анализу»

|
Серия: "Физико-математическое наследие: математика (теория чисел)" Исследования Пьера Ферма (1601-1665) составили эпоху в истории теории чисел. Здесь впервые из многочисленных вопросов и задач были выделены те основные проблемы, которые сделались предметом изучения математиков на протяжении ближайших 200 лет. Некоторые из предложений Ферма до сих пор еще не доказаны. В книге собраны и прокомментированы все тексты Ферма, относящиеся к теории чисел и решению неопределенных уравнений, а именно его замечания к "Арифметике" Диофанта, выдержки из писем, относящиеся к рассматриваемым вопросам, а также трактат Жака де Бильи, в котором изложены методы Ферма решения неопределенных уравнений степеней 2, 3 и 4 в рациональных числах. Для специалистов-математиков, а также для преподавателей вузов и средних школ, студентов университетов, пединститутов и вузов. Перевод с французского и латыни. Издание стереотипное. Издательство: "URSS" (2015)
ISBN: 978-5-382-01620-7 Купить за 507 руб в My-shop |
Ферма П.
Пьер де Ферма́ (фр. Pierre de Fermat, 1601—1665) — французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года — советник парламента в Тулузе. Блестящий полиглот. Наиболее известен формулировкой Великой теоремы Ферма.
Содержание |
Биография
Пьер Ферма родился 17 августа 1601 года в гасконском городке Бомон-де-Ломань (Франция). Его отец, Доминик Ферма, был зажиточным торговцем, вторым городским консулом; мать, Клер де Лонг — преподавательница математики. В семье, кроме Пьера, были ещё один сын и две дочери. Ферма получил юридическое образование — сначала в Тулузе, а затем в Бордо и Орлеане.
В 1631 году, успешно закончив обучение, Ферма выкупил должность королевского советника парламента (другими словами, члена высшего суда) в Тулузе. В этом же году он женился на дальней родственнице матери, Луизе де Лонг. У них было пятеро детей[1].
Быстрый служебный рост позволил Ферма стать членом Палаты эдиктов в городе Кастр (1648). Именно этой должности он обязан добавлением к своему имени признака знатности — частицы de; с этого времени он становится Пьером де Ферма.
Около 1652 года Ферма пришлось опровергать сообщение о своей кончине во время эпидемии чумы; он действительно заразился, но выжил.
В 1660 году планировалась его встреча с Паскалем, но из-за плохого здоровья обоих учёных встреча не состоялась[1].
Пьер де Ферма умер 12 января 1665 года в городе Кастр, во время выездной сессии суда. Первоначально его похоронили там же, в Кастре, но вскоре (1675) прах перенесли в семейную усыпальницу Ферма, в церкви августинцев (Тулуза). Старший сын, Клеман-Самуэль, издал посмертное собрание его трудов, из которого современники и узнали о замечательных открытиях Пьера Ферма.
Современники характеризуют Ферма как честного, аккуратного, уравновешенного и приветливого человека, блестяще эрудированного как в математике, так и в гуманитарных науках, знатока многих древних и живых языков, на которых он писал неплохие стихи.[2]
Научная деятельность

Работа советника в парламенте города Тулузы не мешала Ферма заниматься математикой. Постепенно он приобрёл славу одного из первых математиков Франции, хотя и не писал книг (научных журналов ещё не было), ограничиваясь лишь письмами к коллегам. Среди его корреспондентов были Р. Декарт, Ж. Дезарг, Ж. Роберваль и другие.
Открытия Ферма дошли до нас благодаря сборнику его обширной переписки (в основном через Мерсенна), изданной посмертно сыном Ферма.
В отличие от Галилея, Декарта и Ньютона, Ферма был чистым математиком — первым великим математиком новой Европы. Независимо от Декарта он создал аналитическую геометрию. Раньше Ньютона умел использовать дифференциальные методы для проведения касательных, нахождения максимумов и вычисления площадей. Правда, Ферма, в отличие от Ньютона, не свёл эти методы в систему, однако Ньютон позже признавался, что именно работы Ферма подтолкнули его к созданию анализа [3].
Но главная его заслуга — создание теории чисел.
Теория чисел
Математики Древней Греции со времён Пифагора коллекционировали диковинные факты о конкретных натуральных числах, иногда очень больших, но теорем о числах не доказывали (за несколькими исключениями). Лишь Диофант (III век н. э.) написал книгу «Арифметика», в которой были и отрицательные числа, и элементы символики, но, прежде всего, многочисленные факты о решении в целых числах алгебраических уравнений с несколькими неизвестными (их стали называть диофантовыми). Эта книга (не полностью) стала известна в Европе в XVI веке, а в 1621 году она была издана во Франции и стала настольной книгой Ферма.
Ферма постоянно интересовался арифметическими задачами, обменивался сложными задачами с современниками. Например, в своём письме, получившем название «Второго вызова математикам» (февраль 1657), он предложил найти общее правило решения уравнения Пелля ax2 + 1 = y2 в целых числах. В письме он предлагал найти решения при a=149, 109, 433. Полное решение задачи Ферма было найдено лишь в 1759 году Эйлером.
Начал Ферма с задач про магические квадраты и кубы, но постепенно переключился на закономерности натуральных чисел — арифметические теоремы. Несомненно влияние Диофанта на Ферма, и символично, что он записывает свои удивительные открытия на полях «Арифметики».
Ферма обнаружил, что если a не делится на простое число p, то число ap − 1 − 1 всегда делится на p (см. Малая теорема Ферма). Позднее Эйлер дал доказательство и обобщение этого важного результата: см. Теорема Эйлера.
Обнаружив, что число 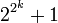 простое при k ≤ 4, Ферма решил, что эти числа простые при всех k, но Эйлер впоследствии показал, что при k=5 имеется делитель 641. До сих пор неизвестно, конечно или бесконечно множество простых чисел Ферма.
простое при k ≤ 4, Ферма решил, что эти числа простые при всех k, но Эйлер впоследствии показал, что при k=5 имеется делитель 641. До сих пор неизвестно, конечно или бесконечно множество простых чисел Ферма.
Эйлер доказал (1749) ещё одну гипотезу Ферма (сам Ферма редко приводил доказательства своих утверждений): простые числа вида 4k+1 представляются в виде суммы квадратов (5=4+1; 13=9+4), причём единственным способом, а для чисел вида 4k+3 такое представление невозможно. Эйлеру это доказательство стоило 7 лет трудов; сам Ферма доказывал эту теорему косвенно, изобретённым им индуктивным "методом бесконечного спуска". Этот метод был опубликован только в 1879 году; впрочем, Эйлер восстановил суть метода по нескольким замечаниям в письмах Ферма и неоднократно успешно его применял. Позже усовершенствованную версию метода применяли Пуанкаре и Андре Вейль.
Ферма разработал способ систематического нахождения всех делителей числа, сформулировал теорему о возможности представления произвольного числа суммой не более четырех квадратов (теорема Лагранжа о сумме четырех квадратов).
Ферма занимали «невозможные» задачи — задачи, не имеющие решений. Самое знаменитое утверждение о «невозможности» — Великая теорема Ферма (ВТФ).
Многие арифметические открытия Ферма опередили время и были забыты на 70 лет, пока ими не заинтересовался Эйлер, опубликовавший систематическую теорию чисел. Одна из причин этого - интересы большинства математиков переключились на математический анализ.
Математический анализ и геометрия
Ферма практически по современным правилам находил касательные к алгебраическим кривым. Именно эти работы подтолкнули Ньютона к созданию анализа[3].
В учебниках по математическому анализу можно найти важную лемму Ферма, или необходимый признак экстремума: в точках экстремума производная функции равна нулю.
Ферма сформулировал общий закон дифференцирования дробных степеней и распространил формулу интегрирования степени на случаи дробных и отрицательных показателей.
Развив идею Декарта, Ферма применил аналитическую геометрию к пространству. В работе «Введение к теории плоских и пространственных мест», ставшей известной в 1636 году, Ферма показал, что прямым соответствуют уравнения 1-й степени, а коническим сечениям — уравнения 2-й степени. Ферма исследовал общие виды уравнений 1-й и 2-й степеней.
Другие достижения
Независимо от Паскаля Ферма разработал основы теории вероятностей. Именно с переписки Ферма и Паскаля (1654), в которой они, в частности, пришли к понятию математического ожидания и теоремам сложения и умножения вероятностей, отсчитывает свою историю эта замечательная наука. Результаты Ферма и Паскаля были приведены к книге Гюйгенса «О расчётах в азартной игре» (1657), первом руководстве по теории вероятностей.
Имя Ферма носит основной принцип геометрической оптики, в силу которого свет в неоднородной среде выбирает путь, занимающий наименьшее время (впрочем, Ферма считал, что скорость света бесконечна, и формулировал принцип более туманно). С этого тезиса начинается история главного закона физики — принципа наименьшего действия.
Ферма перенёс на трёхмерный случай (внутреннего касания сфер) алгоритм Виета для задачи Аполлония (касания окружностей).[4]
Великая теорема Ферма
Ферма широко известен благодаря т. н. великой (или последней) теореме Ферма. Теорема была сформулирована им в 1637 году, на полях книги «Арифметика» Диофанта с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы привести его на полях.
Вероятнее всего, его доказательство не было верным, так как позднее он опубликовал доказательство только для случая n = 4. Доказательство, найденное в 1994 году Эндрю Уайлсом, содержит 129 страниц и опубликовано в журнале «Annals of Mathematics» в 1995 году.
Простота формулировки этой теоремы привлекла много математиков-любителей, так называемых ферматистов. Даже и после решения Уайлса во все академии наук идут письма с «доказательствами» великой теоремы Ферма.
Примечания
- ↑ 1 2 Стиллвелл Д. Математика и ее история. - Москва-Ижевск: Институт компьютерных исследований, 2004, стр. 211-212.
- ↑ Белл Э. Т. Указ. соч., стр. 58.
- ↑ 1 2 С. И. Вавилов. Исаак Ньютон. 2-е дополненное издание. М.-Л.: Изд. АН СССР, 1945 г., глава 13.
- ↑ Барабанов О.О., Барабанова Л.П. Алгоритмы решения навигационной разностно-дальномерной задачи – от Аполлония до Коши // История науки и техники, 2008, №11, С.2-21.
См. также
Литература
Сочинения
- Ферма П. Исследования по теории чисел и диофантову анализу. М.: Наука, 1992.
О нём
- Башмакова И. Г. Диофант и Ферма (к истории метода касательных и экстремумов). Историко-математические исследования, 17, 1966, с. 185–207.
- Башмакова И. Г., Славутин Е. И. История диофантова анализа от Диофанта до Ферма. М.: Наука, 1984.
- Белл Э. Т. Творцы математики. М.: Просвещение, 1979. Глава 4: Ферма.
- Ван дер Варден Б. Л. Переписка между Паскалем и Ферма по вопросам теории вероятностей. ИМИ, 21, 1976, с. 228–232.
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука, 1970. Том 2: Математика XVII столетия.
- Фрейман Л. С. Ферма, Торричелли, Роберваль. В кн.: У истоков классической науки. М.: Наука, 1968, с. 173–254.
Ссылки
- Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Ферма, Пьер в архиве MacTutor
- The Life and times of Pierre de Fermat (1601—1665) from W. W. Rouse Ball’s History of Mathematics
- The Mathematics of Fermat’s Last Theorem
- Fermat’s Achievements
Источник: Ферма П.
Другие книги схожей тематики:
| Автор | Книга | Описание | Год | Цена | Тип книги |
|---|---|---|---|---|---|
| П. Ферма | Исследования по теории чисел и диофантову анализу | Исследования Пьера Ферма составили эпоху в истории теории чисел. Здесь впервые из многочисленных вопросов и… — ЛКИ, (формат: 60x90/16, 320 стр.) Физико-математическое наследие: математика (теория чисел) Подробнее... | 2015 | 1123 | бумажная книга |
| П. Ферма | Исследования по теории чисел и диофантову анализу | Исследования Пьера Ферма составили эпоху в истории теории чисел. Здесь впервые из многочисленных вопросов и… — ЛКИ, (формат: 60x90/16, 320 стр.) Физико-математическое наследие: математика (теория чисел) Подробнее... | 2015 | 696 | бумажная книга |
| Ферма П. | Исследования по теории чисел и диофантову анализу | Исследования Пьера Ферма (1601-1665) составили эпоху в истории теории чисел. Здесь впервые из многочисленных… — URSS, Физико-математическое наследие: математика (теория чисел) Подробнее... | 2015 | 507 | бумажная книга |
| П. Ферма | Исследования по теории чисел и диофантову анализу | Исследования Пьера Ферма (1601-1665) составили эпоху в истории теории чисел. Здесь впервые из многочисленных… — URSS, (формат: 60x90/16, 320 стр.) Подробнее... | 2015 | 435 | бумажная книга |
См. также в других словарях:
Ферма, Пьер — Пьер де Ферма Pierre de Fermat Дата рождения … Википедия
Пьер Ферма — Пьер де Ферма (фр. Pierre de Fermat, 1601 1665) французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года советник парламента в Тулузе.… … Википедия
Ферма Пьер — Пьер Ферма Пьер де Ферма (фр. Pierre de Fermat, 1601 1665) французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года советник парламента в… … Википедия
Ферма П. — Пьер Ферма Пьер де Ферма (фр. Pierre de Fermat, 1601 1665) французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года советник парламента в… … Википедия
