Книга: Н. Бурбаки «Группы и алгебры Ли»

|
Серия: "-" Книга входит в завоевавшую мировое признание энциклопедию современной математики Элементы математики>, созданную группой французских ученых, выступающих под псевдонимом Н. Бурбаки. В 1972 г. издательством Мир>был выпущен перевод гл. IV-VI книги Группы и алгебры Ли>, а сейчас предлагается перевод ее начальных глав (в таком же порядке выходили французские издания). Книга отражает самые современные результаты в этой области. В нейимеется обширный материал по теории алгебр Ли, свободных алгебр Ли и групп Ли. Книга предназначена для широкого круга математиков различных специальностей - от студентов до научных работников. Воспроизведено в оригинальной авторской орфографии издания 1976 года (издательство "Мир" ). Издательство: "ЁЁ Медиа" (1976)
ISBN: 978-5-458-31387-2 Купить за 1691 руб в My-shop |
Другие книги автора:
| Книга | Описание | Год | Цена | Тип книги |
|---|---|---|---|---|
| Теория множеств | Настоящее издание представляет собой перевод первой книги первой части трактата Н. Бурбаки "Начала… — Либроком, (формат: 60x90/16, 458 стр.) Физико-математическое наследие: математика (история математики) Подробнее... | бумажная книга | ||
| Функции действительного переменного | Группа французских математиков, объединенная под псевдонимом «Бурбаки», поставила перед собой цель —… — Главная редакция физико-математической литературы издательства "Наука", (формат: 60x90/16, 412 стр.) Элементы математики Подробнее... | бумажная книга | ||
| Очерки по истории математики | Предлагаемая читателям книга является частью многотомного сочинения "Элементы математики", выпускаемого… — Либроком, (формат: 60x90/16, 296 стр.) Физико-математическое наследие: математика (история математики) Подробнее... | бумажная книга | ||
| Интегрирование. Векторное интегрирование. Мера Хаара. Свертка и представления | Настоящее издание посвящено вопросам математического и векторного интегрирования, мере Хаара, сверстке и… — Главная редакция физико-математической литературы издательства "Наука", (формат: 60x90/16, 320 стр.) Подробнее... | бумажная книга | ||
| Функции действительного переменного. Элементарная теория | Перевод с французского Е. И. Стечкиной. Воспроизведено в оригинальной авторской орфографии издания 1965 года… — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Спектральная теория | Воспроизведено в оригинальной авторской орфографии издания 1972 года (издательство "Наука" ) — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Основные структуры анализа. Книга 1. Теория множеств | Трактат Н. Бурбаки "Начала математики" имеет целью изложить всю современную математику с единой и… — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Общая топология. Основные структуры | В этом новом издании сделано довольно большое число изменений в деталях; кроме того, переделан весь план гл. I… — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Коммутативная алгебра | Воспроизведено в оригинальной авторской орфографии издания 1971 года (издательство "Мир" ) — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Группы и алгебры Ли | Книга входит в завоевавшую мировое признание энциклопедию современной математики "Элементы математики"… — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Алгебра | Группа французских математиков, объединенных под псевдонимом "Бурбаки", поставила перед собой цель —… — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Очерки по истории математики | Предлагаемая читателям книга является частью многотомного сочинения "Элементы математики", выпускаемого… — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Группы и алгебры Ли | Воспроизведено в оригинальной авторской орфографии издания 1986 года (издательство "Мир" ) — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Группы и алгебры Ли | Книга входит во всемирно известную энциклопедию современной математики Основы математики>, созданную… — ЁЁ Медиа, - Подробнее... | бумажная книга | ||
| Алгебра | Содержит современное, и в то же время достаточно элементарное, детальное изложение основных разделов… — ЁЁ Медиа, - Подробнее... | бумажная книга |
Н. Бурбаки
Николя́ Бурбаки́ (фр. Nicolas Bourbaki) — коллективный псевдоним группы французских математиков (позднее в нее вошли несколько иностранцев), созданной в 1935 году.

Целью группы является написание серии книг, отражающих современное состояние математики. Книги Бурбаки написаны в строгой аксиоматической манере и имеют целью дать замкнутое изложение математики на основе теории множеств Цермело-Френкеля (в доработке Бернайса и Гёделя). На группу огромное влияние оказала немецкая математическая школа — Д.Гильберт, Г.Вейль, Дж. фон Нейман (особенно алгебраисты Э.Нётер, Э.Артин и Б. Л.ван дер Варден).
Содержание |
Состав группы
Основателями группы, участвовавшими в её первой встрече, являются:
- Анри Картан (Henri Cartan),
- Клод Шевалле (Claude Chevalley),
- Жан Кулон (Jean Coulomb),
- Жан Дельсарт (Jean Delsarte),
- Жан Дьёдонне (Jean Dieudonné),
- Шарль Эресманн (Charles Ehresmann),
- Рене де Поссель (René de Possel),
- Шолем Мандельбройт (Szolem Mandelbrojt),
- Андре Вейль (André Weil).
Кроме них в первой встрече группы участвовали, но в дальнейшем не принимали участия в её работе, Жан Лере (Jean Leray) и Поль Дюбрейль (Paul Dubreil).
Кроме уже названных, в работе группы в разное время принимали участие многие выдающиеся математики:
- Лоран Шварц,
- Жан-Пьер Серр,
- Александр Гротендик
- Джон Тэйт
- Самуэль Эйленберг
- Серж Ленг
- Пьер Самюэль
- Арман Борель
и другие.
Точный состав и численность группы всегда сохранялись в секрете.
История группы
Группа Бурбаки официально называется Association des collaborateurs de Nicolas Bourbaki (ассоциация сотрудников Николя Бурбаки). Группа была образована выпускниками университета «Высшая Нормальная школа» (École Normale Supérieure) на базе этого же университета. Так как происхождение или работа многих членов группы была связана с городом Нанси, то псевдонимом стала фамилия известного в этом городе генерала Шарля-Дени Бурбаки, в значительной степени из-за греческого происхождения последнего (намёк на древнегреческую математику, особенно на «Начала» Евклида — трактат самих «Бурбаков» носит название «Начала математики», хотя на русский язык это название обычно переводят как «Элементы математики» за исключением «Теории множеств»). Местом жительства Бурбаки был определен город «Нанкаго», то есть Нанси + Чикаго (В Чикаго работали в военное и послевоенное время многие участники группы).
Одним из условий членства в группе был возраст, не превышающий 50 лет. Можно было быть исключённым и раньше, если прочие участники считали, что исключаемый перастал быть творчески работающим математиком. Для этого существовала специальная процедура, носящая название «кокотизация». В основе этого лежит обычай одного из племён Полинезии определять дееспособность своих стареющих вождей — тот должен суметь залезть на пальму и сорвать кокосовый орех. У Бурбаков кокотизация заключалась в следующем: испытуемому описывают какое-нибудь очень сложно определяемое математическое понятие, причём само понятие крайне примитивное, например, число 0, множество целых чисел и т. д. Если испытуемый не сможет догадаться о чём речь, он считается кокотизированным и выбывает из группы, хотя может и участвовать в её организационных или коммерческих мероприятиях. Расцвет группы пришёлся на 1950—1960-е года. Влияние Бурбаки на мировую математику было огромным во Франции, большим в Бельгии, Швейцарии и Италии, довольно значительным в США, и менее значительным в Англии. В СССР к ним относились скорее скептически.
Кризис
Однако приближался кризис. Однажды появилось следующее сообщение в дадаистком стиле:
Семейства Канторов, Гильбертов, Нётеров; семейства Картанов, Шевалле, Дьёдонне, Вейлей; семейства Брюа, Диксмье, Самюэлей, Шварцев; семейства Картье, Гротендиков, Мальгранжей, Серров; семейства Демазюров, Дуади, Жиро, Вердье; семейства, фильтрующиеся вправо, семейства точных эпиморфизмов, мадемуазель Адель и мадемуазель Идель с прискорбием сообщают Вам о смерти мсьё Николя Бурбаки, их отца, брата, сына, внука, правнука и кузена соответственно, скончавшегося 11 ноября 1968 в годовщину Победы в Первой мировой войне в своём доме в Нанкаго. Кремация состоится в субботу, 23 ноября 1968 в 15 часов на «Кладбище случайных величин», станции метро Марков и Гёдель. Сбор состоится перед баром «У прямых произведений» перекрёсток проективных резольвент, бывшая площадь Косуля. Согласно воле покойного месса состоится в соборе «Богоматери универсальных конструкций», месса будет проведена кардиналом Алефом 1 в присутствии представителей всех классов эквивалентностей и алгебраически замкнутых тел. За минутой молчания будут наблюдать ученики Высшей нормальной школы и классов Чженя. Поскольку Бог есть компактификация Александрова для Вселенной — Евангелие от Гротендика, IV,22 [1]
Казалось, это было просто шуткой, но действительно, между членами группы начался разлад[2], причём совпавший с кризисом всей академической науки во Франции особенно усилившимся после Парижской весны 1968. Гротендик, один из величайших учёных XX века, ушёл из группы и вообще из активной математики, другие стали уделять коллективной работе меньше внимания. Книги «Элементов математики» стали выходить значительно реже, на «Семинаре Бурбаки» доклады стали делать учёные меньшего ранга. Последним опубликованным выпуском является[3] глава 10 «Коммутативной алгебры», увидевшая свет в 1998.
Книги Бурбаки
Имея целью создать полностью самодостаточную интерпретацию математики, основанную на теории множеств, группа публикует трактат Éléments de mathématique («Элементы математики» или, более точно, «Начала математики»). Трактат состоит из двух частей. Первая часть носит название Les structures fondamentales de l’analyse — «Основные структуры анализа» и содержит следующие работы (в скобках приведены оригинальные французские названия и их сокращенные обозначения):
- I Теория множеств (Théorie des ensembles — E )
- II Алгебра (Algèbre — A )
- III Топология (Topologie générale — TG )
- IV Функции действительного переменного (Fonctions d’une variable réelle — FVR )
- V Топологические векторные пространства (Espaces vectoriels topologiques — EVT )
- VI Интегрирование (Intégration — INT )
Позже стали выходить книги второй части:
- (без номера) Коммутативная алгебра (Algèbre commutative — AC )
- (без номера) Дифференцируемые и аналитические многообразия (Variétés différentielles et analytiques — VAR ) — вышла только сводка результатов
- (без номера) Группы Ли (Groupes et algèbres de Lie — LIE )
- (без номера) Спектральная теория (Théories spectrales — TS ) — вышла только одна глава
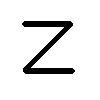
В книгах Бурбаки были впервые введены символ для пустого множества Ø; символы N, Z, Q, R, C для множеств натуральных, целых, рациональных, действительных и комплексных чисел; термины инъекция, сюръекция и биекция; знак «опасный поворот» на полях книги, показывающий, что данное место в доказательстве может быть неправильно понято. Этот знак использует также известный теоретик-программист Д.Кнут.
Критика «бурбакизма»
Представители современной математики часто критикуют подход, представленный в книгах Бурбаки, ныне называемый «бурбакизмом», обвиняя его в излишней заформализованности и «истреблении духа математики». Действительно, участники группы, как правило, были сторонниками чистой математики. Большинство членов группы не уделяло достаточного внимания таким разделам математики, как дифференциальные уравнения, теория вероятностей или математическая физика, не говоря уже о разделах прикладной математики, таких как численные методы или математическое программирование. В наибольшей степени это относится к их коллективному трактату.
Одним из наиболее заметных критиков бурбакизма в России является академик В. И. Арнольд. Так в одной из своих статей[4] Арнольд пишет: «…Действительно, для Бурбаки все общие понятия важнее их частных случаев, поэтому все нестрогие неравенства являются фундаментальными, а строгие — маловажными специальными случаями, примерами…». Однако точка зрения Арнольда не всегда бывает нейтральной и взвешенной: «…Вот почему бурбакистская мафия, заменяющая понимание науки формальными манипуляциями с непонятными „коммутативными“ объектами, так сильна во Франции, и вот что угрожает и нам в России».
Тем не менее, следует признать, что книги Бурбаки оказали значительное влияние на современную математику, и авторитет учёных, составлявших группу, бесспорно признаётся современным математическим сообществом.
Аналогичные группы математиков
Группа математиков Рурского университета издавала свои труды под псевдонимом «Бото фон Кверенбург». Советские математики М.Г.Крейн и И.Ц.Гохберг много работали в соавторстве и назывались вместе «Гокр».
Ссылки
- ↑ Смерть Бурбаки fr:Nicolas Bourbaki#Histoire de Bourbaki
- ↑ А. Гротендик Урожаи и посевы. — Ижевск: Регулярная и хаотическая динамика, 2001. — 288 с.
- ↑ Согласно официальному сайту.
- ↑ В. И. Арнольд «МАТЕМАТИЧЕСКАЯ ДУЭЛЬ ВОКРУГ БУРБАКИ», Вестник РАН, том 72 (2002), N 3, с.245-250.
- Официальная страница Ассоциации Бурбаки(фр.)
- А. Б. Сосинский «Умер ли Никола Бурбаки?», «Математическое Просвещение», Третья серия, Выпуск 2, 1998.
- С. С. Кутателадзе «Апология Евклида»// Владикавказский математический журнал, том 8 (2006), N 2.
Источник: Н. Бурбаки
См. также в других словарях:
Группы Ли — Группой Ли над полем K ( или ) называется группа G, снабжённая структурой дифференцируемого (гладкого) многообразия над K, причём отображения и , определённые так … Википедия
ЛИ АЛГЕБРА АНАЛИТИЧЕСКОЙ ГРУППЫ — а л г е б р а Л и группы Л и G, определенной над полем k, полным относительно нек рого нетривиального абсолютного значения, алгебра Ли группы G, рассматриваемой как Ли локальная группа. Таким образом, как векторное пространство отождествляется с… … Математическая энциклопедия
КОМПЛЕКСИФИКАЦИЯ ГРУППЫ ЛИ — G над R комплексная группа Ли G С, содержащая Gв качестве вещественной подгруппы Ли и такая, что алгебра Ли группы Gявляется вещественной формой алгебры Ли группы (см. Комплексификация ал гебра Ли). Группа Gпри этом наз. вещественной формой… … Математическая энциклопедия
ПРЕДСТАВЛЕНИЕ АЛГЕБРЫ ЛИ — в векторном пространстве V гомоморфизм r алгебры Ли Lнад полем kв алгебру Ли всех линейных преобразований пространства Vнад k. Два представления и наз. эквивалентными (или изоморфными), если существует изоморфизм , для к рого a(r1 (l) v1).r2(l)a… … Математическая энциклопедия
Представление алгебры Ли — У этого термина существуют и другие значения, см. Представление. Представлением алгебры Ли (точнее, линейным представлением алгебры Ли) называется гомоморфизм из алгебры Ли в полную линейную алгебру преобразований некоторого векторного… … Википедия
ПРЕДСТАВЛЕНИЕ ГРУППЫ — изображение элементов группы матрицами или преобразованиями линейного пространства, при к ром сохраняется исходная групповая структура. Поскольку достаточно хорошо изучены матричные группы, при исследовании произвольной группы стараются… … Физическая энциклопедия
